|
1.2.1 轴线偏心
如图2,建立以电机上导轴承中心为原点,垂直向下的主轴转动中心为oz轴的坐标系,机组轴线上任一点在水平面内的偏心距r=r(z),矢径r与x轴夹角为θ(z)。设轴线均质,单位轴长质量为m0,主轴转动角速度为ω。主轴偏心造成的轴颈对泵导轴承的径向力分量、合力大小及与x轴正向夹角分别为
 (6) (6)
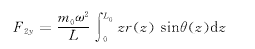 (7) (7)
 (8) (8)
 (9) (9)
式中 L0——电机上导轴承至叶轮中心的轴长
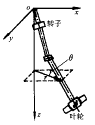
图2 泵机组轴线倾斜偏心
安装要求轴线相对倾斜值r/L0≤0.025 mm/m(转速n≤250 r/min)。
1.2.2 电机转子质心偏心
设电机转子质心偏离转动中心rz, 转子质量mz,转子质心偏心旋转惯性离心力引起的水泵导轴承径向力为
 (10) (10)
由于轴线摆度、磁极不对称和磁轭材质不均匀及温度场不对称等因素造成转子质心偏心。通常,转子可能的最大偏心质量离心力按平衡试加重所产生的离心力确定,其值为转子质量的0.5%~2.5%,
即F3=(0.5%~2.5%)mz g (11)
式中 g——重力加速度
式(11)中系数的取值,低速机组取小值,高速机组取大值。大型立式水泵机组与水轮机相比属高速机组。
1.2.3 水泵叶轮质心偏心
叶轮偏心质量惯性离心力引起的水泵导轴承径向力为
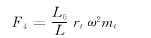 (12) (12)
式中 mt——叶轮质量
rt——叶轮质心偏离转动中心的距离
矢径rt由叶轮材质不均匀和制造误差引起的质心偏离几何中心矢径ro′和叶轮摆度引起的几何中心偏离转动中心矢径ro合成,两矢量在水平面内相加,即
rt=ro′+ro (13)
按要求,叶轮静平衡试验按飞逸时不平衡惯性离心力不超过叶轮重量的2%控制,即
ro′ω2f mt≤0.02mt g
即 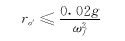 (14) (14)
式中 ωf——机组飞逸角速度
ro为叶轮动摆度值的一半,动摆度与水泵导轴承间隙有关,故ro值为
ro=Sk/2=(Δt-2bm)/2 (15)
式中 Δt——导轴承双边间隙
bm——润滑油膜或水膜厚度
Sk——叶轮动摆度
1.3 横向水力不平衡力的影响
1.3.1 泵轴绕流阻力
立式水泵采用弯管出水,弯管圆心角根据需要确定,常采用π/3或π/2。采用水润滑导轴承的水泵,弯管内泵轴裸露受出水绕流阻力的作用,从而造成水泵导轴承径向力。
见图1,弯管中心线弯曲半径为Rc,泵轴外径为d,弯管内水流速度为vc,泵导轴承中部至弯管起始断面的高度为Ld,泵轴绕流长度为Lr,取距弯管起始断面为y(对应弯管圆心角为α)处微段泵轴dy。此外,水体密度为ρ,泵轴绕流阻力系数为CD,CD与绕流物体形状和雷诺数有关,可查曲线得到。则绕流阻力引起的导轴承径向力为
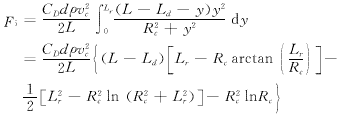 (16) (16)
采用油润滑合金导轴承的水泵,泵轴外设有对开型护管,泵轴不受绕流阻力作用。
1.3.2 水泵叶片角度不等
由于组装误差,导致水泵叶轮数枚叶片角度不等,将所有叶片周向水流阻力向泵轴轴心简化,其结果除水力阻力矩外,还存在垂直于轴线的径向水力不平衡力,该力为所有叶片周向水流阻力的矢量和,即
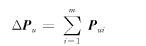 (17) (17)
式中 m——叶轮叶片数
Pui——第i枚叶片水流周向阻力
Pui与Pui+1(i=1,2,…,m-1)夹角为2π/m。
Pui可以采用以下方法计算:
已知水泵运行扬程为H,第i枚叶片角度为αi,认为Pui即为相同泵扬程下所有叶片角度都为αi时的单枚叶片阻力,即
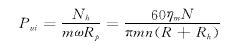 (18) (18)
式中 Nh——泵水力功率
N——轴功率,可由泵性能曲线查得
ηm——泵机械效率,ηm=0.95~0.97[3]
n——水泵转速
R、Rh——叶轮及轮毂半径
显然,角度大的叶片Pui亦大。ΔPu引起的导轴承径向力为
 (19) (19)
一般厂家规定,叶片角度彼此差异最大为1°。
1.3.3 叶轮非轴对称来流
从设计角度考虑,轴流泵叶轮要求来流轴向均匀。但由于流道设计理论的局限性、流道垂直段高度限制(为减小站房基坑开挖深度)和施工误差等原因,叶轮来流往往非轴对称,五孔球探针对大型水泵叶轮来流流场现场测定表明,总流与轴向平均夹角γ为2°~4°[4],水流经过叶轮后成为轴对称,据动量方程可求得该来流作用于叶轮的横向力形成对水泵导轴承的径向力为
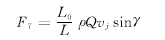 (20) (20)
式中 Q——泵流量 vj——叶轮来流总流流速
2 导轴承荷载确定方法及举例
2.1 导轴承荷载确定
2.1.1 工作荷载
在电机负荷确定的情况下,导轴承分荷载F1与电机相对面最大气隙差值及其所在方位有关。根据造成气隙不均的原因,该方位分为随电机转动变化与不变化两种情形。转动部件偏心引起的分荷载F2、F3、F4及叶轮角度不等引起的F6方向随主轴转动周期性变化。而F5、F7方向分别与水泵出流方向、叶轮来流偏流方向相同,方向不随主轴转动变化。所有分荷载组成水平面内的平面汇交力系。对安装好的机组,各部误差已经确定,某时刻各分荷载大小及方向可以确定,总荷载按所有分荷载进行矢量合成,即
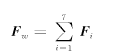 (21) (21)
工作总荷载Fw大小及方向都随时间而变。
2.1.2 设计荷载
在设计水泵导轴承时,一方面因机组制造、安装误差未知,无法确定实际工作荷载大小;另一方面,实际工作荷载大小及方向随时间而变,即使对确定的安装好的机组也难以用表达式准确表示出其与时间的关系。事实上,该关系并不重要。机组各部分制造安装误差大小和方向都是随机的,对水泵导轴承,重要的是确定可能的最大工作荷载,以便以此为依据设计导轴承(偏于保守)。最不利的情况就是引起各分荷载的误差达最大允许值,并且所有分荷载方向相同,此时总荷载最大,即
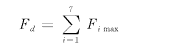 (22) (22)
式中 Fd——设计荷载
Fi max——第i项分荷载最大值
2.2 导轴承设计荷载计算举例
ZL307型立式轴流泵配TL300040/3250型3 000 kW立式同步电动机,转速n=150 r/min,叶轮直径D=3.1 m,轮毂直径Dh=1.668 m,转轮重14 t,泵轴重12 t,转子连轴重19 t。电机定子铁芯高度Hd=0.681 m,定子内径Dd=2.94 m,平均空气间隙δ=4.5 mm,平均磁密B=0.75T,转子偏心距e=0.225mm。各段轴线长度为Lc=1.3 m,L=11.8 m,L0=13.15 m,Lr=3.4 m,Ld=1.2 m。出水弯管中心线弯曲半径Rc=4.2 m,泵扬程H=7 m,泵流量Q=30 m3/s。叶轮有4枚叶片,一枚叶片角度为-1°,其余三枚叶片角度均为0°。叶轮动摆度Sk=0.35 mm,转子及叶轮质心几何偏心方向与摆度方向相同,叶轮来流与轴向夹角γ=3°。
计算结果如下:
F1=10.394 kN F2=0.344 kN
F3=0.331 kN F4=1.906 kN
F5=0.499 kN F6=1.554 kN
F7=6.954 kN
Fd=21.982 kN
由计算结果看出,电机空气间隙对称均匀度、叶轮来流方向、叶轮质心偏心和叶片角度不等对导轴承荷载影响较大。
3 结语
大型立式轴流泵导轴承荷载影响因素多,关系复杂,随机性大。通过对泵机组转动部件横向力分析,本文提出了导轴承荷载计算方法,根据制造安装误差要求及结构,可以对导轴承最大可能荷载进行预测,为导轴承设计提供依据。
导轴承荷载与机组制造安装质量、结构型式及进水流道等因素有关,其中电机空气间隙对称均匀度、叶轮进水流道来流方向、叶轮质心偏心和叶片角度不等的影响较大。为减小导轴承荷载,应严格控制诸方面质量,特别要注意使各因素引起的导轴承径向力方向相反,以相互抵消。同一型号机组,制造安装质量不同,水泵导轴承实际工作荷载差异很大。
本文对立式轴流泵导轴承荷载的分析,有利于从设计、制造、安装各个方面采取综合措施,减小导轴承荷载,延长水润滑非金属导轴承的使用寿命,使其在大型立式水泵中得到广泛应用。
江苏省教委和扬州大学自然科学基金资助项目
仇宝云 扬州大学水利学院 副教授, 225009 江苏省扬州市
参考文献
1,杜刚海 主编. 大型泵站机组安装与检修. 北京: 水利电力出版社, 1995. 75
2,姜培林, 虞烈. 电机不平衡磁拉力及其刚度的计算. 大电机技术, 1998(4): 32~34
3,关醒凡. 泵的理论与设计. 北京: 机械工业出版社, 1987. 312,325~330
4,江苏机电排灌工程研究所. 江都第一抽水站更新改造现场测试报告. 1996. | 
